流程图

范文1 Scenario construction via Delphi and cross-impact analysis 有错误
范文2 A CIA–ISM scenario approach for analyzing complex cascading effects in Operational Risk Management
范文3 Collaborative scenario modeling in emergency management through cross-impact
范文4 A scenario-based model for earthquake emergency management effectiveness evaluation 很明显瞎掰
范文6 Scenario inference model of urban metro system cascading failure under extreme rainfall conditions
CIA (Cross Impact Analysis) 即交叉影响分析
主要是由初始概率P;与发生概率关系矩阵R通过计算得到交叉影响矩阵C,通过对交叉影响矩阵C进行一系列分析的一种方法。
CIA是美国于上世纪60年代,在德尔菲法和主观概率法基础上发展起来的一种新的预测方法。这种方法是主观估计每种新事物在未来出现的概率,以及新事物之间相互影响的概率,对事物发展前景进行预测的方法。
Murray Turoff 提出的CIA有别于其他人提出的CIA,其原理与推导过程在Turoff写的一本关于Delphi方法的书的第五章有非常详细介绍与推导过程。
An Alternative Approach to Cross Impact Analysis
根据流程图以及上面链接所附带的一篇文章。其中R的含义最为关键。
发生概率关系矩阵R为本文的的叫法。也叫相互影响的概率。后续会专门讨论。
ISM (Interpretative Structural Modeling Method) 即解释结构模型
ISM方法是现代系统工程中广泛应用的一种分析方法,是结构模型化技术的一种。一言以蔽之ISM就是在不损失系统功能的前提下给出最简的,层次化的拓扑图。其中最简是求解一般性骨架矩阵(骨干矩阵,骨架矩阵);层次化是通过多种层级抽取的方式获得。
ISM方法是用拓扑层级的方式展示因果层级关系,形象直观。
2003年,黄炜在《黑客与反黑客思维研究的方法论启示——解释结构模型新探》的硕士论文中详细阐述了六种解释结构模型,并给出了界定与命名。
其论文推演的过程为:
先从经典ISM开始,根据不同的情况分别界定了,博弈解释结构模型方法(Game Interpretative Structural Modeling Method, 简称GISM方法)。
模糊解释结构模型方法(Fuzzy Interpretative Structural Modeling Method, 简称FISM方法)把布尔值域,推广到[0,1]范围的模糊论域。
阻尼解释结构模型方法(Damp Interpretative Structural Modeling Method, 简称DISM方法)该方法把[0,1]范围的模糊论域推广到[-1,1]的模糊论域。
虚解释结构模型方法(Virtual Interpretative Structural Modeling Method, 简称VISM方法)把[-1,1]的模糊论域推广的虚数的模糊论域,这只是数学上一种推广,正如作者所言,他也并不清楚这种推广有何现实运用。
函数解释结构模型方法(Function Interpretative Structural Modeling Method, 简称FunISM方法)是一般化的定义,即是一个通式。
其中CIA-ISM方法联用对应的是阻尼解释结构模型,即存在负数的情况
CIA-ISM联用与可视化自动修正简述
从流程图可以看出,联用方法的输入变量为{P,R}
交叉影响矩阵C是ISM方法的输入变量。
SA是一个截距阵,它是布尔矩阵,同普通的布尔矩阵相比,它具有对称结构。
手性拆分是自动可视化修正的关键环节。
通过拆分出来的解耦后的布尔矩阵,可以反推交叉影响矩阵C。
修正后的C可以反推并修正R
核心步骤为如下两步:
R的预估评判与填写,这涉及到需不需要转置的问题
正确的理解手性拆分
交叉影响分析CIA——初始概率P
设系统要素集合为$S=(E1,E2,\ldots ,En)$
其中的要素为事件,其发生情况可以用概率来描述。
$P=\{P1,P2,\ldots ,Pn \}$
初始概率可以通过统计获得,也可以通过常识推导。
交叉影响分析CIA——发生概率关系矩阵R
发生概率关系矩阵R又叫条件概率矩阵:
该关系概率矩阵是由多名专家预测得到。其形式如下:
$$R=\begin{array}{c|c|c|c|c|c|c}{M_{10 \times10}} &E1 &E2 &E3 &E4 &E5 &E6 &E7 &E8 &E9 &E10\\ \hline E1 &0 &0.45 & \color{red}{0} &0.4 &0.45 &0.75 &0 &0.45 &0.45 &0\\ \hline E2 &0.25 &0 &0.28 &0.35 &0 &0.2 &0.38 &0.35 &0.35 &0.34\\ \hline E3 &0.55 &0.65 &0 &0.65 &0.7 &0.5 &0 &0.65 &0.65 &0.66\\ \hline E4 &0.4 &0.6 &0.51 &0 &0.55 &0.3 &0.53 &0.55 &0.55 &0.53\\ \hline E5 &0.3 &0.5 &0.39 &0.5 &0 &0.35 &0.47 &0 &0 &0.43\\ \hline F6 &0.4 &0.25 &0 &0.1 &0.25 &0 &0.27 &0.25 &0.25 &0.27\\ \hline E7 &0.55 &0.75 &0 &0.7 &0.75 &0.55 &0 &0 &0 &0.66\\ \hline E8 &0.1 &0.15 &0 &0.25 &0.25 &0.1 &0 &0 &0.3 &0.24\\ \hline E9 &0.05 &0 &0 &0.15 &0 &0.05 &0.15 &0.2 &0 &0.15\\ \hline E10 &0.55 &0.75 &0.59 &0.7 &0.75 &0.5 &0.66 &0 &0 &0\\ \hline \end{array} $$
$$P=\begin{array}{c|c|c|c|c|c|c}{M_{1 \times10}} &E1 &E2 &E3 &E4 &E5 &E6 &E7 &E8 &E9 &E10\\ \hline P_i &0.50 & 0.30 & 0.60 & 0.50 & 0.40 &0.30 &0.60 &0.20 &0.10 &0.60 \\ \hline \end{array} $$
发生关系概率矩阵解读:
以第一行(E1)第三列(E3)为例子:其意思为,E1事件确定发生,E3发生的概率。当E3的概率等于E1的初始概率的时候设置为0
专家进行评估讨论时候,一个预估的方向为:如E1的初始概率为0.5,E6如果对E1有正影响,则E6的发生概率要大于E1的初始概率0.5,如果是负影响则发生概率要小于0.5
时序有关即时间发生顺序的概率事件中关系概率的特定预估
假定系统有10个事件同时间序列相关
初始事件(Initial Conditions)分别为:$IE1,IE2,IE3,IE4$
动态事件,中间事件(Dynamic Events)分别为:$DE1,DE2,DE3,DE4$
结果事件 (Outcome Events)分别为:$OE1,OE2$
发生概率关系矩阵有如下形式:
$$R=\begin{array}{c|c|c|c|c|c|c}{M_{10 \times10}} & IE1 & IE2 &IE3 & IE4 & DE1 & DE2 & DE3 & DE4 & OE1 & OE2\\ \hline IE1 & x & x &x & x &0 & 0 & 0 & 0 &0 &0\\ \hline IE2 & x & x &x & x &0 & 0 & 0 & 0 &0 &0\\ \hline IE3 & x & x &x & x &0 & 0 & 0 & 0 &0 &0\\ \hline IE4 & x & x &x & x &0 & 0 & 0 & 0 &0 &0\\ \hline DE1 & x & x &x & x &x & x & x & x &0 &0\\ \hline DF2 & x & x &x & x &x & x & x & x &0 &0\\ \hline DE3 & x & x &x & x &x & x & x & x &0 &0\\ \hline DE4 & x & x &x & x &x & x & x & x &0 &0\\ \hline OE1 & x & x &x & x &x & x & x & x &0 &0\\ \hline OE2 & x & x &x & x &x & x & x & x &0 &0\\ \hline \end{array} $$
如上是标准格式,这种格式右边为0的部分不需要填写。
以IE行 到OE列为例子,意思是结果事件,即处于时序末尾的事件对起始事件是不会有任何影响的。
这种填写方式后续进行ISM计算分析时候需要转置,它的好处是右边两列可以不填写排版可以紧凑
发生概率关系矩阵有如下形式:
$$R=\begin{array}{c|c|c|c|c|c|c}{M_{10 \times10}} & IE1 & IE2 &IE3 & IE4 & DE1 & DE2 & DE3 & DE4 & OE1 & OE2\\ \hline IE1 & x & x &x & x &x & x & x & x &x &x\\ \hline IE2 & x & x &x & x &x & x & x & x &x &x\\ \hline IE3 & x & x &x & x &x & x & x & x &x &x\\ \hline IE4 & x & x &x & x &x & x & x & x &x &x\\ \hline DE1 & 0 & 0 &0 & 0 &x & x & x & x &x &x\\ \hline DF2 & 0 & 0 &0 & 0 &x & x & x & x &x &x\\ \hline DE3 & 0 & 0 &0 & 0 &x & x & x & x &x &x\\ \hline DE4 & 0 & 0 &0 & 0 &x & x & x & x &x &x\\ \hline OE1 & 0 & 0 &0 & 0 &0 & 0 & 0 & 0 &0 &0\\ \hline OE2 & 0 & 0 &0 & 0 &0 & 0 & 0 & 0 &0 &0\\ \hline \end{array} $$
上述格式更符合ISM原始关系矩阵的定义与习惯如动态事件DE1从逻辑上来说对初始事件是无影响,因此DE所在的行,起始事件IE所在的列的概率关系为0
这种填写方式后续进行ISM计算分析时候不需要转置
总之R的评估是整个CIA-ISM计算的最重要的部分。
P与R是整个CIA-ISM的输入,前提条件,也是后续修正的基础。
交叉影响分析CIA——交叉影响矩阵C
求解公式
$$ C_{ij}= \frac {1}{1-P_j}[ln( \frac {R_{ij}}{1-R_{ij}} ) - ln(\frac {P_i}{1-P_i} )] $$
交叉影响矩阵C与发生概率关系矩阵G的关联
$(P , R) \Longrightarrow C$
$ R \Longleftarrow (C,P)$
推导过程如下:
$C_{ij} - C_{ij}P_j=ln( \frac {R_{ij}}{1-R_{ij}} ) - ln(\frac {P_i}{1-P_i} )$
$C_{ij} - C_{ij}P_j+ ln(\frac {P_i}{1-P_i} )=ln( \frac {R_{ij}}{1-R_{ij}} ) $
$e^{C_{ij} - C_{ij}P_j+ ln(\frac {P_i}{1-P_i} )}= \frac {R_{ij}}{1-R_{ij}} $
$e^{-[C_{ij} - C_{ij}P_j+ ln(\frac {P_i}{1-P_i} )]}= \frac {1}{R_{ij}} -1 $
$\frac{1+e^[C_{ij} - C_{ij}P_j+ ln(\frac {P_i}{1-P_i} )]}{e^[C_{ij} - C_{ij}P_j+ ln(\frac {P_i}{1-P_i} )]}= \frac {1}{R_{ij}} $
$R_{ij} = \frac{ e^[C_{ij} - C_{ij}P_j+ ln(\frac {P_i}{1-P_i} )]}{1+e^[C_{ij} - C_{ij}P_j+ ln(\frac {P_i}{1-P_i} )]}$
$$ R_{ij} = \frac{ P_i e^{C_{ij}(1-P_j)}} {1-P_i+P_i e^{C_{ij}(1-P_j)} } $$
由C求解发生概率关系矩阵,是能可视化修正R的基石
影响值的正负及含义
C矩阵中的值有正负之分,正表示为正影响。
负表示为负影响。
转置
转置操作同R的格式有关,标准发生概率关系矩阵R的格式,在进行ISM分析时候,需要先转置
请注意转置的先决条件
对称手性矩阵SH
平移对称化——图形化解释
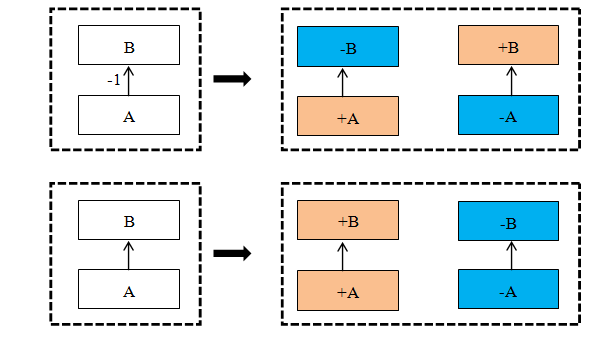
其中箭头为负向,转化成两种对应情况,有向线段的值为正转化得到两种情况。
实例:
$$ C^T=\tilde D=\begin{array} {c|c|c|c}{M_{4 \times4}} & a & b & c & d\\ \hline a &0 &\color{red}{-1.9} &0 &0\\ \hline b & \color{red}{-2.5}&0 &\color{blue}{1.8}&0\\ \hline c &0 &0 &0 &0\\ \hline d &0 &\color{blue}{1.9} &0 &0\\ \hline \end{array}$$
经过平移对称化后得到的对称手性矩阵SH如下:
$$ SH =\begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 & \color{red}{1.9} &0 &0 \\ +b &0 &0 &0.8 &0 & \color{red}{2.5} &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &0.9 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &1.9 &0 &0 &0 &0 &0 &0 \\ -b &2.5 &0 &0 &0 &0 &0 &0.8 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &0.9 &0 &0\\ \hline \end{array} $$平移对称化的代数描述
$$\tilde f_{ij}= \begin{cases} \tilde f_{(-i)(+j)}=|\tilde d_{ij}| 且 \tilde f_{(+i)(-j)}=|\tilde d_{ij}| , \tilde d_{ij}< 0 \\ \tilde f_{(-i)(-j)}=|\tilde d_{ij}| 且 \tilde f_{(+i)(+j)}=|\tilde d_{ij}| , \tilde d_{ij}> 0 \end{cases}$$交叉影响矩阵转置后的矩阵为:$C^T=\tilde D= [ \tilde d ]_{n \times n} $
对称手性矩阵SH为:$SH=\tilde F= [ \tilde f ]_{2n \times 2n} $
SH是对称矩阵,要素数目是是交叉影响矩阵C的两倍
手性一词来自化学学科,指的就是对称行,手性原意是左手与右手一样,是对称的
SH 中的S 为 Symmetrical H 为Hand
对称手性矩阵SH取截距的方式得到手性对称关系矩阵SA
阈值集合的定义
$阈值集合\ddot \Delta$阈值集合为矩阵$SH$中不重复的数值的集合
$$ SH =\begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 & \color{red}{1.9} &0 &0 \\ +b &0 &0 &0.8 &0 & \color{red}{2.5} &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &0.9 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &1.9 &0 &0 &0 &0 &0 &0 \\ -b &2.5 &0 &0 &0 &0 &0 &0.8 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &0.9 &0 &0\\ \hline \end{array} $$
其阈值集合为 $ \ddot \Delta = (0,0.8, 0.9, 1.9, 2.5) $
阈值集合中元素的数量要大于等于最终的的层级拓扑结构
其中,$\lambda 1,\lambda 2,\cdots,\lambda n $ 为的阈值集合中的元素
通常存在着 $ SA_j SA_k $ 为同构。且 j k对应为相邻的区域
实例: 截距为0通常不计算在内
$$ SH =\begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 & \color{red}{1.9} &0 &0 \\ +b &0 &0 &0.8 &0 & \color{red}{2.5} &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &0.9 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &1.9 &0 &0 &0 &0 &0 &0 \\ -b &2.5 &0 &0 &0 &0 &0 &0.8 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &0.9 &0 &0\\ \hline \end{array} $$
$$ SA_{1}=SH_{0.8} =\begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 & \color{red}{1} &0 &0 \\ +b &0 &0 &0 &0 & \color{red}{1} &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &1 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &1 &0 &0 &0 &0 &0 &0 \\ -b &1 &0 &0 &0 &0 &0 &0 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &1 &0 &0\\ \hline \end{array} $$
$$ SA_{2}=SH_{0.9} =\begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 & \color{red}{1} &0 &0 \\ +b &0 &0 &0&0 & \color{red}{1} &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &0 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &1 &0 &0 &0 &0 &0 &0 \\ -b &1 &0 &0 &0 &0 &0 &0 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &0 &0 &0\\ \hline \end{array} $$
$$ SA_{3}=SH_{1.9} =\begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 & 0 &0 &0 \\ +b &0 &0 &0&0 & \color{red}{1} &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &0 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &0 &0 &0 &0 &0 &0 &0 \\ -b &1 &0 &0 &0 &0 &0 &0 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &0 &0 &0\\ \hline \end{array} $$
$$ SA_{4}=SH_{2.5} =\begin{array} {c|cccc|cccc}{M_{8 \times8}} & +a &+b &+c &+d &-a &-b &-c &-d\\ \hline +a &0 &0 &0 &0 &0 & 0 &0 &0 \\ +b &0 &0 &0&0 & 0 &0 &0 &0 \\ +c &0 &0 &0 &0 &0 &0 &0 &0\\ +d &0 &0 &0 &0 &0 &0 &0 &0\\ \hline -a &0 &0 &0 &0 &0 &0 &0 &0 \\ -b &0 &0 &0 &0 &0 &0 &0 &0 \\ -c &0 &0 &0 &0 &0 &0 &0 &0\\ -d &0 &0 &0 &0 &0 &0 &0 &0\\ \hline \end{array} $$
可以观察到当截距为0时候,得到的关系矩阵 通常为满阵
当截距为阈值集合中最大值时候,得到的关系矩阵为零阵
从图形特征走向来看是从一个大回路 变到 完全离散的系统
ISM的运算步骤
核心是一般性骨架矩阵求解与层级划分

对抗层级拓扑方式

对抗层级拓扑方式

对称层级拓扑的特征
非连通性对称拓扑,不需要手性拆分
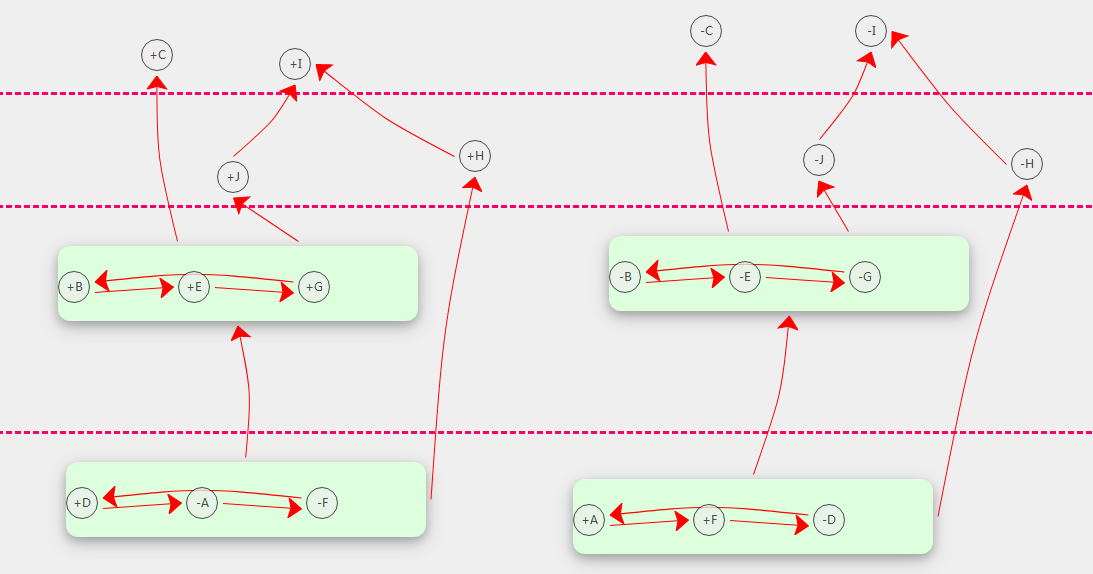
上面层级拓扑图为非连通性对称拓扑,其最大连通域为对称型。
连通性对称拓扑,需要手性拆分
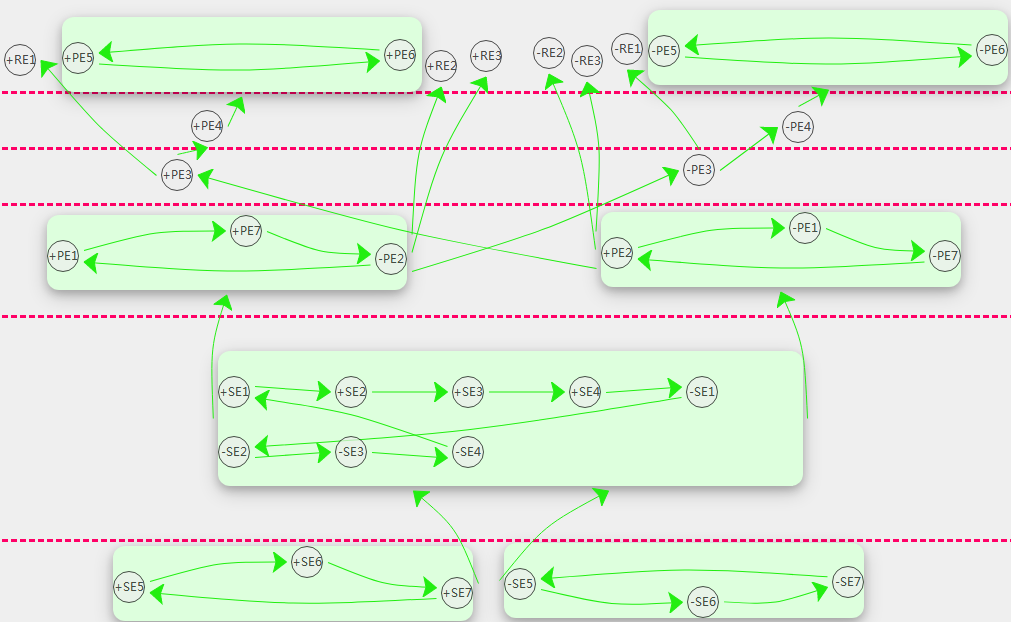
上面层级拓扑图为连通性对称拓扑,需要进行手性拆分。
手性拆分
手性拆分的理由
构成系统的要素是事件来描述。对于事件是以概率来揭示事物的本质。对于一个事件来说,概率的增加于概率的减少只能取一种状态。不会有同时是增加又是减少的情况。
手性拆分一词的来源
手性拆分一词来源于化学学科,最早来自巴斯德发现手性晶体(酒石酸晶体)。
手性拆分拆分的原则
第一、连通性的对称结构才需要进行手性拆分
第二、要素的正负,事件的正负,只能取一种状态,即某一个要素取了正,就不能取负。
第三、拆分出来的结构,结构层次不发生变化
例子1
需要拆分的结构如下:
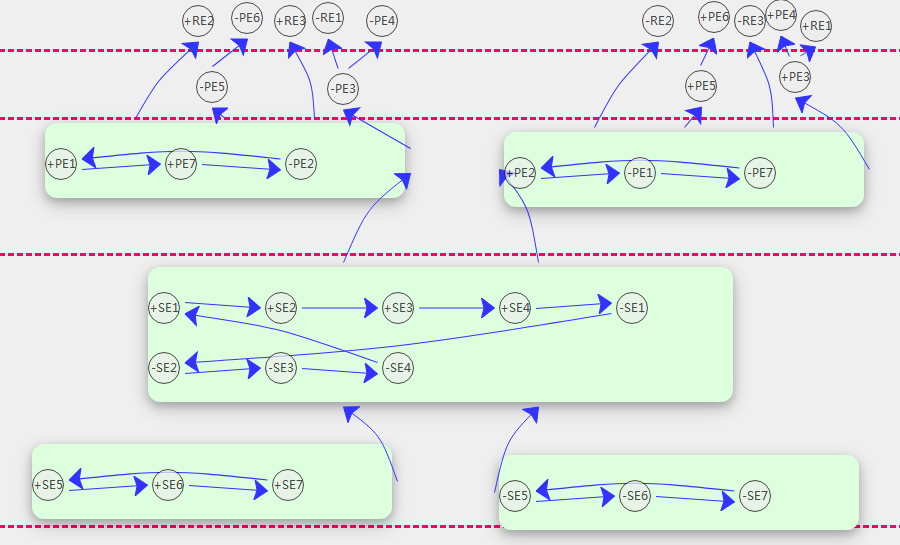
拆分后的结构形式如下:
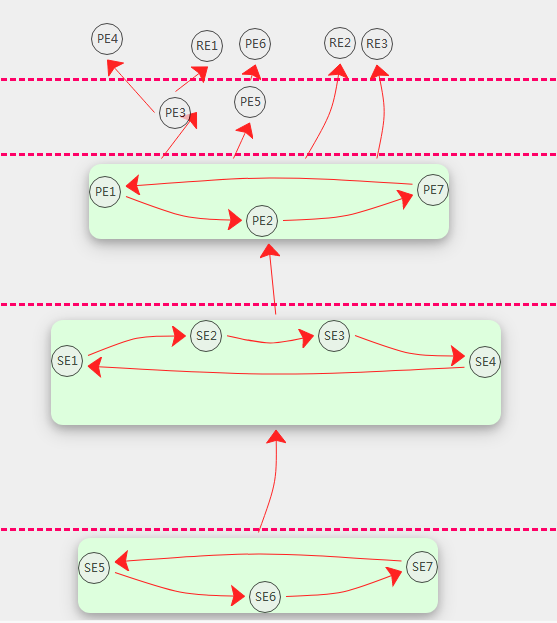
例子2
拆分前的对称结构如下:
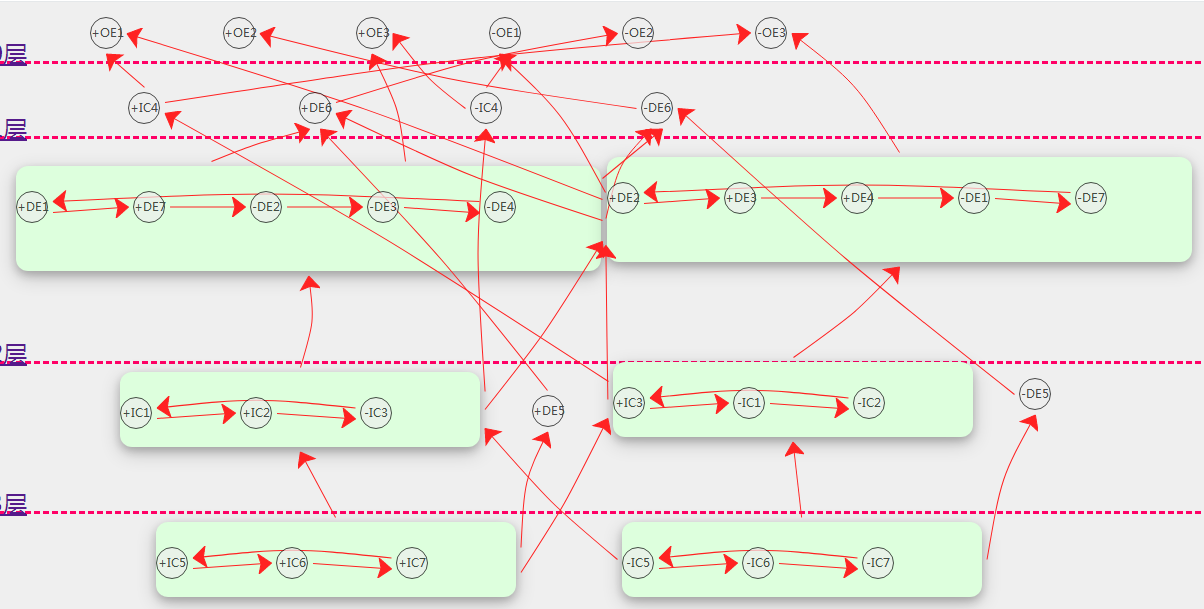
对照结构形式如下:
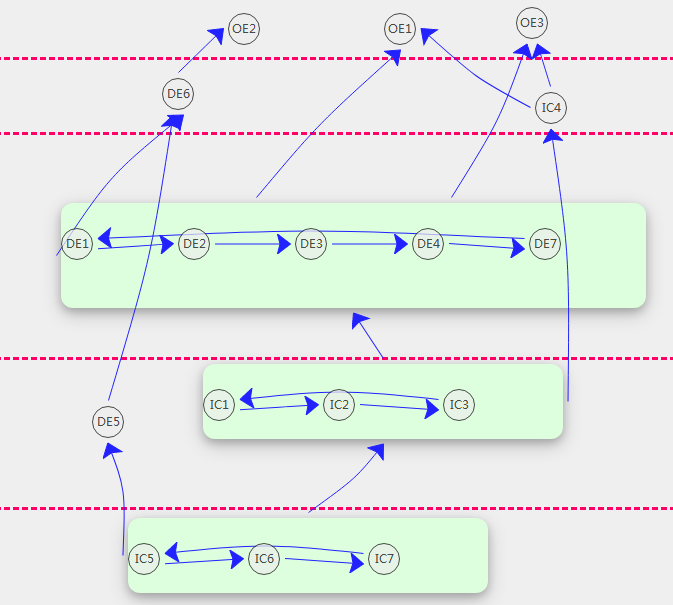
错误的拆分结果:
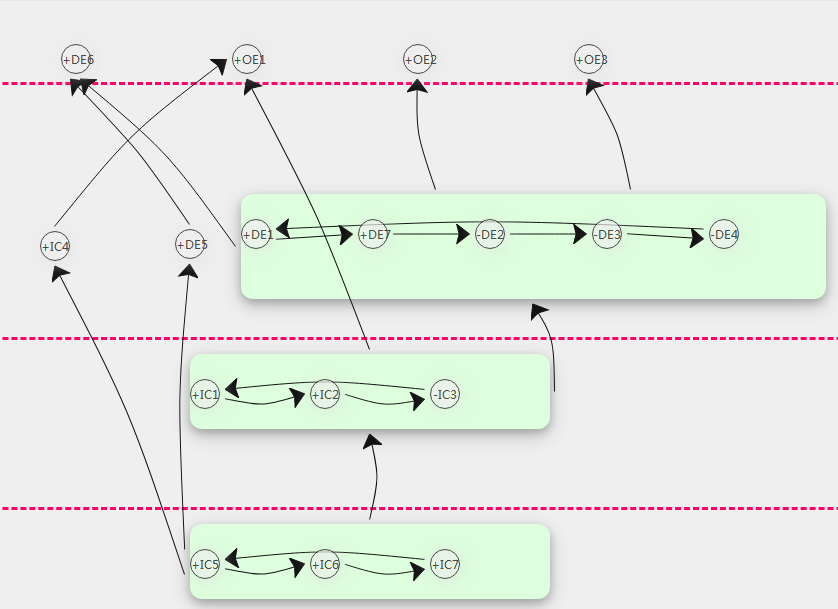
正确的拆分结果:
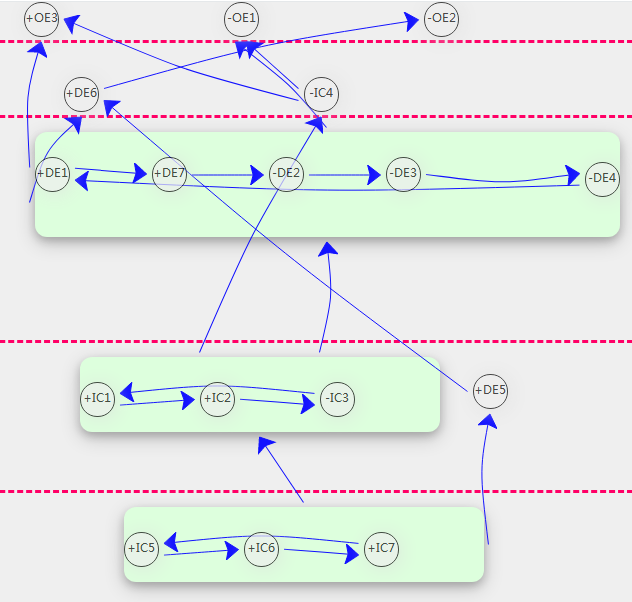
手性中心与拆分后的对称结构的数目
手性中心
手性中心的概念源自化学学科。通常指一个碳原子连着4个不同的基团,该碳原子称之为手性中心。
拓扑结构的手性中心可以简单的理解为:某个要素,其中一个正要素,同时指向另外一个要素的正向或者负向。
更精准的定义需要运用群论来解释与计算。
手性中心与拆分后的结构数目
设手性中心的数目为 $x$
拆分出的对称结构的数目为 $Y$
两者的关系为$Y=2^x$
设:C矩阵的要素数目为$n$,SA矩阵的要素数目则为 $2n$
取截距为0,该布尔矩阵为满阵,进行拆分后的的对称结构的数目为 $Y$
两者的关系为$Y=2^n$
自动拆分运算量非常大很难实现
曾经试图通过一个SA的矩阵,以及C取绝对值对应的截距阵,获得的层级结构,进行拆分处理。
这玩意是个NP-hard问题。
这玩意花了我好几年的时间,专门写自动拆分。然并卵,网页经常卡死。
最终处理成半自动,或者把判断拆分的主动权交到研究者手上。
因此一定注意拆分的准则。
解耦后的层级图对R的自动修正
选哪个截距值开始进行手性拆分
理论上是越小越好,即选择截距$\lambda=0$
实际上是选择一个没有强连通对称单元的SA开始进行手性拆分。
强连通对称单元是啥?
设在层级结构中存在着一个回路,且要素X在该回路中
当$+X,-X$都在该回路中,这个回路称为强连通单元或者叫强回路
例子见下图
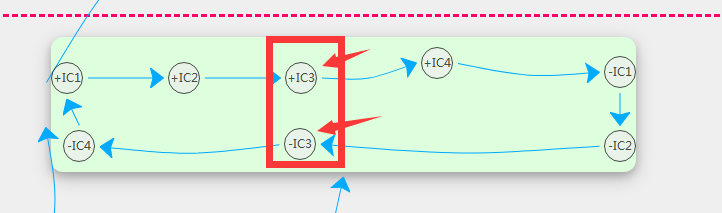
回路中只要一个要素的正负都处于该回路,由于对称性原理,其它要素的正负必定处于该强回路中
数据修正过程
设手性拆分后的解耦结构对应的布尔矩阵为$Z$该矩阵为一个布尔矩阵
求出该$Z$矩阵对应的可达矩阵$RZ$
由$RZ$中为0的位置,逐个检索$C^T$中的值,并取绝对值,如果其大于当前的截距值$t$则修改成该截距值即可
由$C,P$得到R
自动修正完毕。
CIA-ISM相关讨论
发展历程
2003年,黄炜在《黑客与反黑客思维研究的方法论启示——解释结构模型新探》中提出了DISM(阻尼解释结构模型),CIA-ISM就是DISM的一种形式。
2011年在《Scenario construction via Delphi and cross-impact analysis》一文中Murray Turoff等第一次提出了交叉影响分析-解释结构模型方法。
该文标志着CIA-ISM方法的诞生。
该文强调了场景一词。更关键的是,该文有原始数据,计算过程详细,且每一步都可以验证。
截止2022年,以CIA-ISM方法的文章并不多,估计不超过10篇。但是发表的期刊都还可以。
Scenario construction via Delphi and cross-impact analysis 讲解
论文网址Scenario construction via Delphi and cross-impact analysis
该文的P,R的数据来源:An Alternative Approach to Cross Impact Analysis
其中R的数据来源如下:
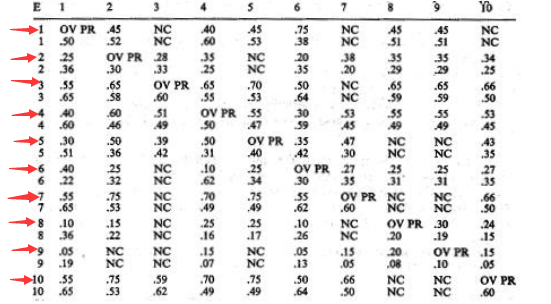
上图为发生概率关系矩阵与不发生概率关系矩阵合并,取第一部分。
其中C矩阵如下:
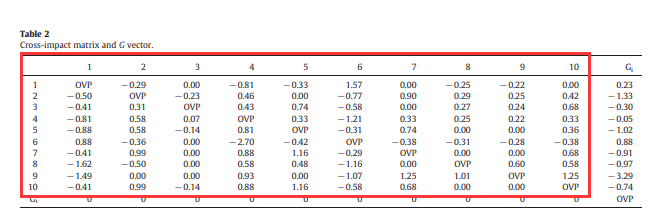
经过校验,该论文没有算错。计算与校验地址
论文中由table2即交叉影响矩阵C通过平移对称化取截距0.85得到SA矩阵
SA矩阵如下:
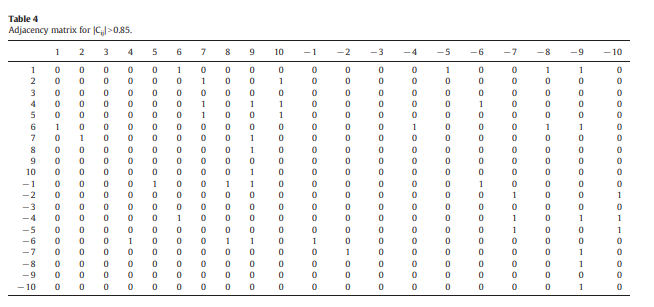
老头这篇开创性的文章,遗漏了转置这关键性的步骤。
按照论文的说法,table2是无法得到table4的。table2需要转置、平移交叉对称化,取截距才能得到table4
论文table4对应的层级拓扑只取了一半的要素,具体见如下对比图
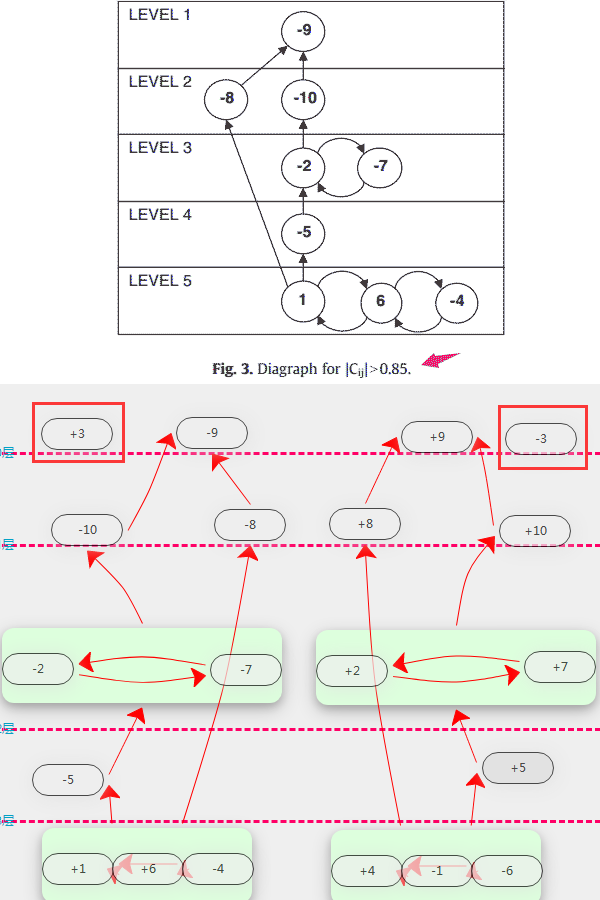
通过比对发现,论文中没有把 +3与-3要素列出。
此外老头选取的结构都是非连通对称结构,即不需要拆分。
计算地址及说明
计算与自动修正: 核心步骤为手性拆分