DEMATEL起源

　　Decision-making Trial and Evaluation Laboratory(DEMATEL)直译为决策实验室分析。

　　DEMATEL也有翻译成决策与试验评价实验室，或者简称实验室法。由于中文比较拗口，一般情况下，念[de mei tel] 或者念 [di mie tel]。

　　1971年在日内瓦的一次会议上美国Battelle实验室的学者A. Gabus和E. Fontela提出的为了解现实世界中复杂、困难的问题而提出的方法论，是一种运用图论和矩阵工具的系统分析的方法。

　　通过系统中各要素之间的逻辑关系和直接影响矩阵，可以计算出每个要素对其它要素的影响度以及被影响度，从而计算出每个要素的原因度与中心度，作为构造模型的依据，从而确定要素间的因果关系和每个要素在系统中的地位。

△Battelle不要写成Bastille 后者是巴士底狱的意思，也是一个著名的乐队。不少文章介绍都写错了。巴特尔的含义很广，详情可参考百度百科跟维基百科

DEMATEL建模的实质

DEMATEL建模的实质是把系统看成一个带权值的有向图。

　带权值的有向图

带权值的有向图是一种图示法

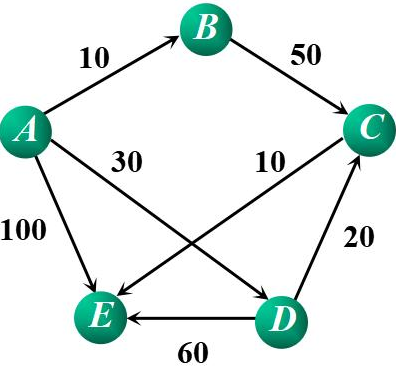
在上图中可以观察到带权值的有向图有三个特点

第一、 在系统中由节点组成，节点又称为要素。

第二、 系统通常是一个连通图。两个要素之间若存在联系，其中一个要素是发出箭头，另外一个要素是接收箭头。

第三、 边上有数值。该数值通常是某一要素对另外一要素的强度。也是可以是具体的物理单位，如力的单位牛顿等等

带权值的有向图跟矩阵对应

上图的矩阵表示如下：

# 矩阵形式 说明
1 $M=\begin{vmatrix} 0 & 10 & 0 & 30 & 100 \\ 0 & 0 & 50 & 0 & 0\\ 0 & 0 & 0 & 0 & 10\\ 0 & 0 & 20 & 0 & 60\\ 0 & 0 & 0 & 0 & 0\\ \end{vmatrix} $ 两边为直线
2 $M=\begin{bmatrix} 0 & 10 & 0 & 30 & 100 \\ 0 & 0 & 50 & 0 & 0\\ 0 & 0 & 0 & 0 & 10\\ 0 & 0 & 20 & 0 & 60\\ 0 & 0 & 0 & 0 & 0\\ \end{bmatrix} $ 用中括号表示
3 $M=\begin{pmatrix} 0 & 10 & 0 & 30 & 100 \\ 0 & 0 & 50 & 0 & 0\\ 0 & 0 & 0 & 0 & 10\\ 0 & 0 & 20 & 0 & 60\\ 0 & 0 & 0 & 0 & 0\\ \end{pmatrix} $ 用小括号
4 $M=\begin{Bmatrix} 0 & 10 & 0 & 30 & 100 \\ 0 & 0 & 50 & 0 & 0\\ 0 & 0 & 0 & 0 & 10\\ 0 & 0 & 20 & 0 & 60\\ 0 & 0 & 0 & 0 & 0\\ \end{Bmatrix} $ 大括号
5 $M=\begin{Vmatrix} 0 & 10 & 0 & 30 & 100 \\ 0 & 0 & 50 & 0 & 0\\ 0 & 0 & 0 & 0 & 10\\ 0 & 0 & 20 & 0 & 60\\ 0 & 0 & 0 & 0 & 0\\ \end{Vmatrix} $ 两条竖线
6 $ M=\begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 10 & 0 & 30 & 100 \\ \hline B & 0 & 0 & 50 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 10\\ \hline D & 0 & 0 & 20 & 0 & 60\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array} $ 表格形式加上表头可以对齐
7 $ M=\begin{array} {c|ccccccc} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 10 & 0 & 30 & 100 \\ \hline B & 0 & 0 & 50 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 10\\ \hline D & 0 & 0 & 20 & 0 & 60\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array} $ 只加横线的表示方式
8 $ M=\begin{array} {c|ccccccc} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & & 10 & & 30 & 100 \\ \hline B & & & 50 & & \\ \hline C & & & & & \\ \hline D & & & 20 & & 60\\ \hline E & & & & & \\ \hline \end{array} $ 矩阵中为零的值用空白表示
9 $ M=\begin{array} {c|ccccccc} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & - & 10 & - & 30 & 100 \\ \hline B & - & - & 50 & - & -\\ \hline C & - & - & - & - & 10\\ \hline D & - & - & 20 & - & 60\\ \hline E & - & - & - & - & -\\ \hline \end{array} $ 矩阵中为零的值用短横线表示表示

上面展示的就是矩阵的一般表示形式。


  DEMATEL原始矩阵有如下几个要点：

第一、 该矩阵的名称又叫关系矩阵，指要素之间的关系。

第二、 矩阵的值不能为负数。出现负数为及特殊的情况需要专门建模。

第三、 对角线的取值为零,其意义为要素本身不参与比较与判断。

第四、 矩阵为方阵，行与列对应的是同一个要素。

第五、 当要素很大的时候尽量用表格型的矩阵表示方式，这样便于核对。

第六、 上述矩阵中第一行，第二列的值为10，其意义为：第一行对应的要素A对第二列对应的要素B发出一个箭头，该边的值为10。

　DEMATEL实施步骤

　　第一步：从研究目的出发，确定研究指标或元素。量化各元素之间的相互关系。得到直接影响矩阵。

　　第二步：通过归一化原始关系矩阵。得到规范直接影响矩阵。

　　第三步：由规范化直接影响矩阵。计算得到综合影响矩阵。。

　　第四步：由综合影响矩阵。得到各个要素的影响度、被影响度、中心度、原因度。

　　第五步：由计算得出的中心度于原因度绘图，并作出解释，根据实际情况进行进一步的处理，如去除非核心要素，与解释结构模型(ISM)等系统方法联用。

　　　　直接影响矩阵获得

　

　　DEMATEL方法中最重要的一步就是直接影响矩阵的获得。

　　系统科学认为，系统是要素之间有机的联系在一起。DEMATEL是一个系统分析方法。它首先把系统分为了要素和要素跟要素之间的联系。因此DEMATEL要获得直接影响矩阵，有如下几个步骤

  1. 　所分析系统各个要素的确定。
  2. 　要素之间的二元关系的确定。通常是两两比较。其中要素$S_i$ 跟要素$S_j$ 要比较两次，分别是要素$S_i$ 对要素$S_j$ 的直接影响；要素$S_j$ 对要素$S_i$ 的直接影响。对于整个系统来说存在n个要素则要比较n(n-1)次。而要素自身则不需要比较，即矩阵的对角线上的值通常用0来表示。
  3. 　关系强弱的度量方法的确定。

　　在上述步骤中关系强弱的度量方法通常有如下几种。

  1. 　客观的具有极强精度的测量值的量其值取一个自然数。如长度，等等物理量。
  2. 　10级标度，即取0-9的方法来度量
  3. 　5级标度，即取0-4的方法来度量。此方法为最常见采用的方法。

　　由于事物具有模糊性，采用精确的度量方法无意义。通常采用的方法是诸如：{没有,较小,一般,较大,非常大}、{无,很弱,正常,较强,很强}等语义来度量要素相互之间的强弱。

  • 　 $ \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 10 & 0 & 30 & 100 \\ \hline B & 0 & 0 & 50 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 10\\ \hline D & 0 & 0 & 20 & 0 & 60\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array} \longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 1\\ \hline D & 0 & 0 & 1 & 0 & 3\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}=\mathcal{M} $

　　　　规范影响矩阵

　

　　归一化是对事物标准化的常规操作。如平均数就是一个典型的归一化的操作。进行归一化最关键的是要以一个最大值作为标准。

　　直接影响矩阵 $\mathcal{M}$。则定义$\mathcal{M}$中的值用${a_{ij}}$表示：$\mathcal{M}={(a_{ij})_{n \times n}}$

　$$ Maxvar=max(\sum_{j=1}^n {a_{ij}} )$$

　　在矩阵中即每一行求和，在这些值中取出最大值。

  • 　 $ \mathcal{M}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 1\\ \hline D & 0 & 0 & 1 & 0 & 3\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}\longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E & \color{red}{Sum} \\ \hline A & 0 & 1 & 0 & 2 & 4 & \color{red}{7} \\ \hline B & 0 & 0 & 3 & 0 & 0 & \color{red}{3}\\ \hline C & 0 & 0 & 0 & 0 & 1 & \color{red}{1}\\ \hline D & 0 & 0 & 1 & 0 & 3 & \color{red}{4}\\ \hline E & 0 & 0 & 0 & 0 & 0 & \color{red}{0}\\ \hline \end{array} $
  • $\\ \\ Maxvar=max(7,3,1,4,0)=7 \\$

　　规范直接影响矩阵定义$\mathcal{N}$ 则：$\mathcal{N}=\left( {a_{ij}} \over Maxvar \right)_{n \times n}$

  • 　 $ \mathcal{M}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 1\\ \hline D & 0 & 0 & 1 & 0 & 3\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}\longrightarrow \mathcal{N}=\begin{array} {|c|c|c|c|c|c|c|c|} \hline {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1\over \color{red}{7} & 0 & 2\over \color{red}{7} & 4\over \color{red}{7} \\ \hline B & 0 & 0 & 3\over \color{red}{7} & 0 & 0 \\ \hline C & 0 & 0 & 0 & 0 & 1\over \color{red}{7} \\ \hline D & 0 & 0 & 1\over \color{red}{7} & 0 & 3\over \color{red}{7} \\ \hline E & 0 & 0 & 0 & 0 & 0 \\ \hline \end{array} $
  • 　最终有 $ \mathcal{N}=\begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 0.1429 & 0 & 0.2857 & 0.5714 \\ \hline B & 0 & 0 & 0.4286 & 0 & 0 \\ \hline C & 0 & 0 & 0 & 0 & 0.1429 \\ \hline D & 0 & 0 & 0.1429 & 0 & 0.4286 \\ \hline E & 0 & 0 & 0 & 0 & 0 \\ \hline \end{array} $

归一化的的影响矩阵求解非常容易，核心在于最大值的获取方法。

还是上面的图，如果线的权值表示的是同一量纲的精确的物理量。直接影响矩阵可以直接用原来的数值。

  • 　 $ \mathcal{M}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 10 & 0 & 30 & 100 \\ \hline B & 0 & 0 & 50 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 10\\ \hline D & 0 & 0 & 20 & 0 & 60\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array} \longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E & \color{red}{Sum} \\ \hline A & 0 & 10 & 0 & 30 & 100 & \color{red}{140} \\ \hline B & 0 & 0 & 50 & 0 & 0 & \color{red}{50}\\ \hline C & 0 & 0 & 0 & 0 & 10 & \color{red}{10}\\ \hline D & 0 & 0 & 20 & 0 & 60 & \color{red}{80}\\ \hline E & 0 & 0 & 0 & 0 & 0 & \color{red}{0}\\ \hline \end{array} $
  • $\\ \\ Maxvar=140 \\$
  • $ \mathcal{N}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 10\over \color{red}{140} & 0 & 30\over \color{red}{140} & 100\over \color{red}{140} \\ \hline B & 0 & 0 & 50\over \color{red}{140} & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 10\over \color{red}{140} \\ \hline D & 0 & 0 & 20\over \color{red}{140} & 0 & 60\over \color{red}{140} \\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}\longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 0.0714 & 0 & 0.2143 & 0.7143 \\ \hline B & 0 & 0 & 0.3571 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 0.0714\\ \hline D & 0 & 0 & 0.1429 & 0 & 0.4286\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array} $

　　　　综合影响矩阵

　　综合影响矩阵，英文为total relation matrix故该矩阵通常用$T$来表示。也有用希腊字母$\tau$ 或者 $\Gamma $来表示。

　　规范直接影响矩阵一直自乘后，矩阵所有值会趋近于0，也就是一个零阵。 $\mathcal{O}=\lim \limits_{k \to \infty} {\mathcal{N}^k} $

　　规范直接影响矩阵自乘,表示的是要素之间增加的间接影响！ 当把所有的间接影响都加起来的时候有如下公式。

$$ \require{AMScd} T=(\mathcal{N}+\mathcal{N}^2+\mathcal{N}^3+\cdots+\mathcal{N}^k)=\sum_{k=1}^\infty {\mathcal{N}^k} \begin{CD} @>>>\end{CD}T=\mathcal{N}(I-\mathcal{N})^{-1}$$
  • 其中$ T $为综合影响矩阵
  • $ \mathcal{N} $为规范化影响矩阵
  • $ I $为单位矩阵，即对角线值为1其它地方的值为0的矩阵
  • $ (I-\mathcal{N})^{-1} $为$(I-\mathcal{N})$的逆矩阵。

　　用软件工具求解逆矩阵

　　逆矩阵的求解是DEMATEL方法中最复杂与繁琐的一步计算。也是DEMATEL方法中最核心的运算步骤。

　　少量的要素情况下如100个以下，通常是用Excel或者Matlab来完成。

　　就直观性与方便性而言，推荐用Excel来完成。

　　在excel中选中矩阵单元格如A1:C3区域。MINVERSE(A1:C3)在另外一个区域按ctrl+shift+entry就完成了逆矩阵的求解。

　　excel的MINVERSE函数中 M表示矩阵， inverse表示求逆。

　　在Matlab中逆矩阵有一个专门的函数来处理。

　　在inv(a)中，a为某矩阵，inv运算后就得到了逆矩阵。

　　LU分解法求逆矩阵原理

　　矩阵$A$是非奇异，也即矩阵是满秩的时候，$A$才是可逆矩阵。矩阵的秩指的是矩阵最大的线性无关的 行或者列的数目。因此对于方阵$A$，只有$A$中不含有线性相关的行或者列的时候方阵$A$才是可逆矩阵，才能求出矩阵$A$的逆矩阵。

　　逆矩阵有多种方法求解，在计算机求解逆矩阵中，用得最多的是LU分解法求解逆矩阵。

　　LU分解法其实是高斯消元法的一种变种算法。

　　是将矩阵A分解为一个下三角矩阵与一个上三角矩阵的乘积。

　　所谓的三角阵就是一半为零的矩阵。

  • L是下三角矩阵(Lower TriangularMatrix)，即主对角线以上的值全部都是0的矩阵。
  • U是上三角矩阵(Upper Triangular Matrix)，即主对角线以下的值全部都是0的矩阵。

　　由定义有:　$$ A=LU$$

　　其逆矩阵有　$$ A^{-1}=L^{-1}U^{-1}$$

$$ A=LU= \begin{vmatrix} 1&0&{\cdots}&0 \\ {l_{21}}&1&{\cdots}& 0\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {l_{n1}}&{l_{n2}}&{\cdots}&1\\ \end{vmatrix} \times \begin{vmatrix} {a_{11}}&{u_{12}}&{\cdots}&{u_{1n}}\\ 0&{u_{22}}&{\cdots}&{u_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ 0&0&{\cdots}&{u_{nn}}\\ \end{vmatrix} $$ 　　上述矩阵中符合如下公式： $$ \left\{ \begin{aligned} u_{1j} &=a_{1j},j\in(1,2,{\cdots},n)\\ l_{i1}&= \frac{a_{i1}}{u_{i1}},i\in(2,{\cdots},n) \\ l_{ik}&= \frac{a_{ik}-\sum \limits_{m=1}^{k-1}l_{im}u_{mk}}{u_{kk}},i\in(k+1,k+2,{\cdots},n);k\in(2,3,{\cdots},n) \\ u_{kj} &= a_{kj}- \sum \limits_{m=1}^{k-1}l_{km}u_{mj} ,j\in(k,k+1,{\cdots},n);k\in(2,3,{\cdots},n) \end{aligned} \right. $$

　　上面的公式其本质属于高斯消元法。对于计算机来说运用LU分解更易于实现并行化计算。

　　诸如求 50000*50000这种大型矩阵。都采用LU分解法来计算！

　　L矩阵求逆公式如下：

$$ (L|I)= \left( \begin {array} {cccc|cccc} l_{11}& -& -&- &1&-&-&-\\ l_{21}& l_{22}& -&- &-&1&-&-\\ {\vdots}& {\cdots}& {\ddots}&- &-&-&1&-\\ l_{n1}&l_{n2}& {\cdots}&l_{nn} &-&-&-&1 \end {array} \right ) $$

　　逆矩阵中的值$(l^{-1})_{ij}$如下：

$$ (l^{-1})_{ij}= \left\{ \begin{array}{ll} 0 & \textrm{, $i < j$}\\ \frac{1}{l_{ii}} & \textrm{, $i = j$}\\ -\frac{1}{l_{ii}} \sum \limits_{k=j}^{i-1} {l_{ik}} {(l^{-1})_{kj}} & \textrm{, $i > j$} \end{array} \right. $$

　　对于任意三角阵其转置矩阵的逆矩阵等于其逆矩阵的转置矩阵:

$$ (L^{\Gamma})^{-1}=(L^{-1})^{\Gamma} $$ $$ (U^{\Gamma})^{-1}=(U^{-1})^{\Gamma} $$

　　因此在求解上三角矩阵的逆矩阵的时候可以先将其转置为下三角矩阵，然后利用求解下三角矩阵的逆矩阵算法来对其进行求解，再对结果进行转置就可以求解出上三角矩阵的逆矩阵。

　　由规范直接影响矩阵到综合影响矩阵算例

  • 计算公式：$T=\mathcal{N}(I-\mathcal{N})^{-1}$
  • 规范直接矩阵 $\mathcal{N}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 0.1429 & 0 & 0.2857 & 0.5714 \\ \hline B & 0 & 0 & 0.4286 & 0 & 0 \\ \hline C & 0 & 0 & 0 & 0 & 0.1429 \\ \hline D & 0 & 0 & 0.1429 & 0 & 0.4286 \\ \hline E & 0 & 0 & 0 & 0 & 0 \\ \hline \end{array} $

  • 单位矩阵 $ \\\\I= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 1 & 0 & 0 & 0 & 0 \\ \hline B & 0 & 1 & 0 & 0 & 0 \\ \hline C & 0 & 0 & 1 & 0 & 0 \\ \hline D & 0 & 0 & 0 & 1 & 0 \\ \hline E & 0 & 0 & 0 & 0 & 1 \\ \hline \end{array} $

  • 单位矩阵-规范直接矩阵 $ I-\mathcal{N}= \begin{vmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{vmatrix}- \begin{vmatrix} 0 & 0.1429 & 0 & 0.2857 & 0.5714 \\ 0 & 0 & 0.4286 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0.1429 \\ 0 & 0 & 0.1429 & 0 & 0.4286 \\ 0 & 0 & 0 & 0 & 0 \\ \end{vmatrix} \\ \\ = \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 1&-0.1429&0&-0.2857&-0.5714 \\ \hline B &0&1&-0.4286&0&0 \\ \hline C & 0&0&1&0&-0.1429 \\ \hline D & 0&0&-0.1429&1&-0.4286 \\ \hline E & 0 & 0 & 0 & 0 & 1 \\ \hline \end{array} $
  • (单位矩阵-规范直接矩阵)的逆矩阵 $$ (I-\mathcal{N})^{-1}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 1&0.1429&0.1021&0.2857&0.7084 \\ \hline B &0&1&0.4286&0&0.06125 \\ \hline C & 0&0&1&0&0.1429 \\ \hline D & 0&0&0.1429&0&0.449 \\ \hline E & 0 & 0 & 0 & 0 & 1 \\ \hline \end{array} $$
  • 综合影响矩阵 $$ T=\mathcal{N}(I-\mathcal{N})^{-1}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A&-&0.1429&0.1021&0.2857&0.7084 \\ \hline B&-&-&0.4286&-&0.0612 \\ \hline C&-&-&-&-&0.1429 \\ \hline D&-&-&0.1429&-&0.4490 \\ \hline E&-&-&-&-&- \\ \hline \end{array} $$

　　　　影响度、被影响度、中心度与原因度

　　影响度、被影响度、中心度与原因度是四种度量要素在系统里影响程度的度量准则。它们都是根据综合影响矩阵计算得出。

　　根据综合影响矩阵$T$中值$t_{ij}$进一步计算出每个要素的影响度、被影响度以及中心度与原因度。

　　$t_{ij}$表示要素$i$对要素$j$所带来的直接影响加上间接影响的程度，即产生的综合影响程度。同时也表示，要素$j$受到要素$i$的综合影响程度。

　　影响度

　　指的是$T$的各行矩阵的值之和表示各行对应要素对所有其他要素的综合影响值，即影响度，该集合记为$D $。

  • $$ D=(D_1,D_2,D_3,\cdots,D_n) $$ 其中： $$ D_i=\sum \limits_{j=1}^{n}{t_{ij}},(i=1,2,3,\cdots,n) $$

　　被影响度

　　指的是$T$的各列的值之和，表示各列对应要素受到所有其他各要素的综合影响值，即被影响度，该集合记为$C $。

  • $$ C=(C_1,C_2,C_3,\cdots,C_n) $$ 其中： $$ C_i=\sum \limits_{j=1}^{n}{t_{ji}},(i=1,2,3,\cdots,n) $$

　　中心度

　　要素 $ i$ 的影响度和被影响度相加得到该要素的中心度记作 $M_i$。中心度表示该因素在评价指标体系中的位置及其所起作用的大小。

  • $$ M_i=D_i+C_i $$

　　原因度

　　要素 $ i$ 的影响度和被影响度相减得到该要素的原因度记作 $R_i$。

  • $$ R_i=D_i-C_i $$

    如果原因度大于0，表明该要素对其他要素影响大，称为原因要素；反之，称为结果因素。

　　影响度、被影响度、中心度与原因度算例

  • 综合影响矩阵 $$ T=\mathcal{N}(I-\mathcal{N})^{-1}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A&-&0.1429&0.1021&0.2857&0.7084 \\ \hline B&-&-&0.4286&-&0.0612 \\ \hline C&-&-&-&-&0.1429 \\ \hline D&-&-&0.1429&-&0.4490 \\ \hline E&-&-&-&-&- \\ \hline \end{array} $$
  • 影响度与被影响度计算 $$ \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E & \color{red}{D} \\ \hline A&-&0.1429&0.1021&0.2857&0.7084 &\color{red}{1.2391} \\ \hline B&-&-&0.4286&-&0.0612 &\color{red}{0.4898} \\ \hline C&-&-&-&-&0.1429 &\color{red}{0.1429} \\ \hline D&-&-&0.1429&-&0.4490 &\color{red}{0.5919} \\ \hline E&-&-&-&-&- &\color{red}{0} \\ \hline \color{blue}{C}&\color{blue}{0}&\color{blue}{0.1429}&\color{blue}{0.6736}&\color{blue}{0.2857}&\color{blue}{1.3616}&- \\ \hline \end{array} $$ $$ \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 2}} & \color{red}{D} & \color{blue}{C}\\ \hline A&\color{red}{1.2391} &\color{blue}{0} \\ \hline B&\color{red}{0.4898} &\color{blue}{0.1429} \\ \hline C&\color{red}{0.1429} &\color{blue}{0.6736}\\ \hline D&\color{red}{0.5919} &\color{blue}{0.2857} \\ \hline E&\color{red}{0} &\color{blue}{1.3616}\\ \hline \end{array} $$
  • 中心度与原因度 $$ \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 4}} & \color{red}{D_i} & \color{blue}{C_i}&M_i&R_i\\ \hline A&\color{red}{1.2391} &\color{blue}{0}&1.2391 &1.2391 \\ \hline B&\color{red}{0.4898} &\color{blue}{0.1429} &0.6327 &0.3469 \\ \hline C&\color{red}{0.1429} &\color{blue}{0.6736}&0.8165 &-0.5307 \\ \hline D&\color{red}{0.5919} &\color{blue}{0.2857} &0.8776 &0.3062 \\ \hline E&\color{red}{0} &\color{blue}{1.3616}&1.3616 &-1.3616 \\ \hline \end{array} $$

　　　　绘图并进行进一步的处理

　　用图表表述方式其效果远高于文字表达。而DEMATEL制成图表有一定难度，其难度在于有向边的绘制。

　　此外从美观角度考虑，在极端情况下，例如系统里的要素完全为一个回路，则有向边完全重叠成了一个点。

　　从软件工具的角度excel与matlab都没有DEMATEL这种散点图跟有向图结合的图表形式。

　　中心性（Centrality）用于分析网络的最广泛使用和最重要的概念工具之一。中心性旨在寻找网络系统中最重要的节点。由于存在对“重要”的不同理解，因此存在许多中心性度量标准。中心性标准本身就可以分成好多类。有一些标准是以沿着边的流动为特征，还有一些标准以步行结构（Walk Structure）为特征。

　　图论中常用的标准有如下：

  • 度中心性（Degree Centrality） - 第一个也是概念上最简单的中心性定义。表示连接到某节点的边数。在有向图中，我们可以有2个度中心性度量。流入和流出的中心性。
  • 紧密中心性（Closeness Centrality） - 从某节点到所有其他节点的最短路径的平均长度。
  • 中介中心性（Betweenness Centrality） - 某节点在多少对节点的最短路径上。

　　DEMATEL最后求出的是四种影响关系，其中心性相关更多的是单个要素在整体系统里的度中心性。在两对关系中：中心度——原因度更受到关注。

　　上图是基于中心度——原因度的笛卡尔直角坐标，其中X轴对应中心度，Y轴对应原因度。

　　要素之间的有向边对应原始矩阵大于0的值。

　　DEMATEL经常用来做要素分析。在判断核心要素与非核心要素的一个原则是中心度，删除非核心要素的规则是看中心度上图越靠左边的值越早删除。

　　如上图中的阈值取0.7，则要素B删除。

  • 中心度阈值取0.4则把中心度小于0.4以下的要素全部删除。
  • 中心度阈值为0.55则把中心度小于0.55以下的要素全部删除。

　　上图是基于影响度——被影响度的笛卡尔直角坐标。

　　这种坐标系，经常用来标注系统的层级阶梯。

　规范影响矩阵的讨论

　　规范影响矩阵采用是归一化的方法，最大值怎么取是最核心的问题。

　　要使得矩阵中的值都变成$[0,1]$的闭区间，可知，$Maxvar$必须大于直接影响矩阵中任何一个值。

　行和最大值法

刚开始介绍的方法就是这种方法。

$$Maxvar=max(\sum_{j=1}^n {a_{ij}} )$$

　列和最大值法

与行和最大值法对应的是列和最大值法

$$Maxvar=max(\sum_{i=1}^n {a_{ij}} )$$
  • $ \mathcal{M}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 1\\ \hline D & 0 & 0 & 1 & 0 & 3\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}\longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0 \\ \hline C & 0 & 0 & 0 & 0 & 1 \\ \hline D & 0 & 0 & 1 & 0 & 3 \\ \hline E & 0 & 0 & 0 & 0 & 0 \\ \hline \color{red}{Sum}& \color{red}{0}& \color{red}{1}& \color{red}{4}& \color{red}{2} & \color{red}{8} \\ \hline \end{array} $
  • $ Maxvar=max(0,1,4,2,8)=8 $

　　行和、列和最大值法

所有的行和与列和取出最大值

$$Maxvar=max(max(\sum_{j=1}^n {a_{ij}} ),max(\sum_{i=1}^n {a_{ij}} ))$$
  • $ \mathcal{M}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 1\\ \hline D & 0 & 0 & 1 & 0 & 3\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}\longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E & \color{red}{Sum} \\ \hline A & 0 & 1 & 0 & 2 & 4 & \color{red}{7} \\ \hline B & 0 & 0 & 3 & 0 & 0 & \color{red}{3}\\ \hline C & 0 & 0 & 0 & 0 & 1 & \color{red}{1}\\ \hline D & 0 & 0 & 1 & 0 & 3 & \color{red}{4}\\ \hline E & 0 & 0 & 0 & 0 & 0 & \color{red}{0}\\ \hline \end{array} \longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0 \\ \hline C & 0 & 0 & 0 & 0 & 1 \\ \hline D & 0 & 0 & 1 & 0 & 3 \\ \hline E & 0 & 0 & 0 & 0 & 0 \\ \hline \color{red}{Sum}& \color{red}{0}& \color{red}{1}& \color{red}{4}& \color{red}{2} & \color{red}{8} \\ \hline \end{array} $
  • $ Maxvar=max(max(7,3,1,4,0),max(0,1,4,2,8))=max(7,8)=8 $

　　　最大值取弦法

把行和最大值，看成直角三角形的一条边，列和最大值看成另外一条边。而直角三角形的斜边也就是弦当成最大值。

$$\overline {a}=max(\sum_{j=1}^n {a_{ij}} )$$ $$\overline {b}=max(\sum_{i=1}^n {a_{ij}} )$$ $$Maxval=\overline {c}=\sqrt{(\overline{a})^2+(\overline{b})^2}$$
  • $ \mathcal{M}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 1\\ \hline D & 0 & 0 & 1 & 0 & 3\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}\longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E & \color{red}{Sum} \\ \hline A & 0 & 1 & 0 & 2 & 4 & \color{red}{7} \\ \hline B & 0 & 0 & 3 & 0 & 0 & \color{red}{3}\\ \hline C & 0 & 0 & 0 & 0 & 1 & \color{red}{1}\\ \hline D & 0 & 0 & 1 & 0 & 3 & \color{red}{4}\\ \hline E & 0 & 0 & 0 & 0 & 0 & \color{red}{0}\\ \hline \end{array} \longrightarrow \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 2 & 4 \\ \hline B & 0 & 0 & 3 & 0 & 0 \\ \hline C & 0 & 0 & 0 & 0 & 1 \\ \hline D & 0 & 0 & 1 & 0 & 3 \\ \hline E & 0 & 0 & 0 & 0 & 0 \\ \hline \color{red}{Sum}& \color{red}{0}& \color{red}{1}& \color{red}{4}& \color{red}{2} & \color{red}{8} \\ \hline \end{array} $
  • $ \overline {a}=max(7,3,1,4,0)=7; \qquad \qquad \overline{b}=max(0,1,4,2,8)=8 $
  • $ \overline {c}=\sqrt{{7^2}+{8^2}}= \sqrt{49+64}= \sqrt{113}= 10.6301 $

　　　其它归一化的方法

　　事实上在获得规范矩阵的方法上有无数种方法。而常用的比较好理解的方法都集中在了跟三角函数相关的方法上。

　　比如最大直角边法就是一种：

  • $ \overline {a}=max(7,3,1,4,0)=7; \qquad \qquad \overline{b}=max(0,1,4,2,8)=8 $
  • $ (\overline {c})^2=max(49+0,9+1,1+16,16+4,0+64)=64 $
  • $ {\overline {c}}=8 $

　　模糊算子相关方法取最大值。模糊算子与三角模紧密相关。

　　比如模糊算子中的爱因斯坦算子的加就是一种：

　　由于涉及到了模糊数学的相关知识，且模糊算子更多的是在模糊数即$[0,1]$闭区间的函数，这里就不再深入描述。

　　总之规范直接影响矩阵的就是归一化的一种，通常采用的方法是于几何相关的线性法则，简单的就是取行和的最大值当成最大值。在某些具有固定物理意义的范畴内，其最大值可以专门指定。

　　比如某场景下，上述值指的是特定的酸碱度的标定。因此最大值就直接取14

  • $\mathcal{M}= \begin{array} {c|c|c|c|c|c|c|c} {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1 & 0 & 7 & 8 \\ \hline B & 0 & 0 & 3 & 0 & 0\\ \hline C & 0 & 0 & 0 & 0 & 1\\ \hline D & 0 & 0 & 1 & 0 & 3\\ \hline E & 0 & 0 & 0 & 0 & 0\\ \hline \end{array}\longrightarrow \mathcal{N}=\begin{array} {|c|c|c|c|c|c|c|c|} \hline {M_{5 \times 5}} & A & B & C & D & E \\ \hline A & 0 & 1\over \color{red}{14} & 0 & 7\over \color{red}{14} & 8\over \color{red}{14} \\ \hline B & 0 & 0 & 3\over \color{red}{14} & 0 & 0 \\ \hline C & 0 & 0 & 0 & 0 & 1\over \color{red}{14} \\ \hline D & 0 & 0 & 1\over \color{red}{14} & 0 & 3\over \color{red}{14} \\ \hline E & 0 & 0 & 0 & 0 & 0 \\ \hline \end{array} $

　DEMATEL核心算法，即矩阵乘法意义的讨论

DEMATEL最核心的步骤为：$$ T=(\mathcal{N}+\mathcal{N}^2+\mathcal{N}^3+\cdots+\mathcal{N}^k)$$

其中：$\mathcal{N}\times\mathcal{N}$ 的意义为增加的间接关系，它即包括直接影响矩阵中不为0的值之间的增加量，也包括通过要素之间的影响的传递导致0值变成了非零的值。

　基于这点有很多学者，根据不同场景的特征提出不同的看法。

　对角线的值的问题

　　归一化的直接影响矩阵的意义从名称即知。指的是要素对要素的直接影响。按照这个逻辑自身到自身应该为1而不是为0。

　　当然有学者反驳，因为规范直接影响矩阵的直接影响关系，包括两个方面，即要素i对要素j的影响与要素j对要素i的影响。两者的关系刚好相反，具体到对角线上则表现为0。

　　如果对角线的值全部为1进行影响的计算，该相乘的运算法则要变成模糊矩阵的自然算子的运算法则。其过程成了FISM模型，具体过程不再描述。

　矩阵相乘的意义

　　通过综合影响矩阵$T$ 获得的方法，可以看出，由直接关系到综合关系的根本假设是：N矩阵不停相乘然后加起来。

　　从方法论上从方法论上看，以及实现的矩阵运算看，它完全是线性的方法。而复杂系统内部因素之间的复杂性、非线性关系。针对这点Michnik 在欧洲运筹学刊物 (EJOR) 上给出 一种改进的 DEMATEL 算法 (即 WINGS 算法 —–weighted influence non-linear gauge system)。该文全名叫Weighted Influence Non-linear Gauge System (WINGS) – An analysis method for the systems of interrelated components

　　该文主要是针对，增加的影响加了一个权值进行运算，具体方法就不再表述。